GCL学术成果:SIGGRAPH Asia 2025- 具有局部最大曲率的G²插值样条
【论文标题】G² Interpolating Spline with Local Maximum Curvature
【作者】蒋博文,陈仁杰* 1
【单位】中国科学技术大学1
背景与问题
曲线设计是计算机图形学中的一项核心技术,广泛应用于动画制作、艺术设计、数据拟合和科学可视化等领域。然而,传统方法往往难以在插值精度、曲率控制与计算效率之间取得良好平衡。近似曲线(如B样条和NURBS)虽具备优秀的平滑性与局部支撑特性,却无法精确穿过控制点,限制了其在需要精确定位的场景中的应用。另一方面,插值曲线虽能确保穿过所有控制点,但在实现高阶连续性(如 G² 连续性)时,常伴随尖点、自交或局部性差等问题。在曲率控制方面,现有方法(如分段螺旋曲线和 κ-curves)虽能将曲率极值对齐至控制点,但通常依赖全局优化且缺乏局部支撑能力。曲线混合方法(如 Yuksel 曲线)虽几何性质良好且无需全局优化,但由于采用固定的三角混合函数,无法在控制点处实现局部曲率极值。因此,开发一种能够同时满足高阶连续性、精确插值、局部曲率控制且支持非迭代计算的曲线设计方法,成为当前计算机图形学领域的一项重要挑战。本研究旨在针对该问题提出一种创新解决方案。
解决方案
我们提出一种新型混合曲线构造方法:每个插值函数仅插值一个控制点,并在该点处实现曲率最大值。通过约束混合函数的边界条件,自然保证曲线的插值性与 G¹ 连续性。进一步,通过推导 G² 连续性和局部曲率极值条件,我们将问题建模为一个约束优化问题。为实现高效的非迭代求解,我们采用四次Bézier样条构造混合函数,成功将控制点处的曲率控制解耦,将原问题转化为 n 个独立的二维子问题,大幅降低了求解复杂度。在此基础上,我们引入曲率参数以增强曲线的表现力。与现有方法相比,仅通过调整曲率参数,即可生成形态多样、复杂且满足 G² 连续性与局部曲率极值条件的曲线。此外,我们还证明了新曲线具备局部支撑、无自交、相邻曲线段互不相交等优良性质,进一步提升了该方法的实用性与可靠性。
实验结果
实验表明,所生成的曲线均满足 G² 连续性,且在每个控制点处取得曲率最大值。在固定控制点配置的前提下,仅通过调整曲率参数,即可灵活调控局部曲线形状:通常情况下,曲率参数越大,曲线越尖锐;参数越小,曲线越平坦。该方法无需多段曲线拼接,即可生成复杂且富有表现力的曲线,充分验证了其在几何设计与控制灵活性方面的优势。
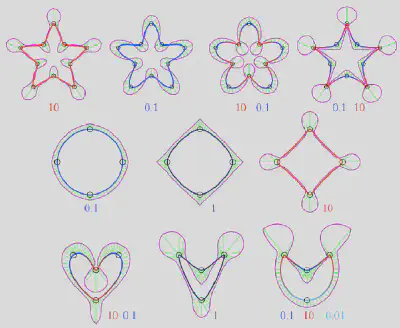
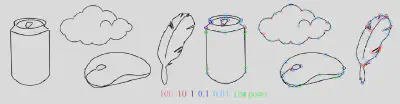

技术贡献
本工作的主要贡献包括以下四个方面:
- 曲线混合与局部曲率控制的统一框架
基于新型曲线混合方法,构建约束优化问题,在严格保证 G² 连续性的同时,实现了控制点处的局部曲率最大化。该框架为混合曲线中的曲率控制问题提供了新的解决思路。
- 高效的非迭代求解机制
借助四次Bézier形式的混合函数,实现了曲率控制的解耦优化,使得每段曲线可在 O(1) 时间复杂度内完成求解,显著提高了计算效率。
- 灵活的曲率调控能力
引入曲率参数,使用户能够连续调整控制点附近曲线的特征,从平滑过渡到尖锐。该机制提供了一种直观的形状控制手段,通过单一参数即可生成多样的几何形态,增强了设计的灵活性与表现力。
- 严格的几何约束保障
建立了一套完善的几何约束体系,在保持局部支撑的同时,确保曲线无自交、相邻段互不交叉。该体系显著提升了曲线的拓扑稳定性,避免了传统方法中因控制点移动而产生的视觉缺陷。
论文发表
该工作已被计算机图形学顶会Siggraph Asia 2025接收,并将发表于顶级期刊《ACM Transactions on Graphics》。该期刊2024-2025年度影响因子为7.8,是计算机科学与软件工程领域的一区刊物之一。
论文原文
Bowen Jiang, Renjie Chen: G² Interpolating Spline with Local Maximum Curvature. ACM Transactions on Graphics (Proc. SIGGRAPH Asia), 44(6), 2025.