GCL学术成果：SIGGRAPH 2025-高阶cage内的双调和坐标

5月 17, 2025 1 分钟阅读时长

【论文标题】Polynomial 2D Biharmonic Coordinates for High-order Cages.

【作者】柳士博，代铁琳，刘利刚，傅孝明

【单位】中国科学技术大学

背景与问题

在计算机图形学领域，重心坐标广泛应用于形状变形等问题。传统的重心坐标主要定义在多边形域上，边界由直线段表示，然而，使用曲线表示域边界可以提供更高的灵活性和保真度，这在众多应用场景中具有关键意义。

近年来，研究者们提出了多种方法来推广重心坐标到曲线边界。其中，广义重心坐标能够精确插值边界，而Green和Cauchy坐标能够产生共形的变形结果，双调和坐标则在边界对齐和变形扭曲控制之间提供了一个良好的平衡方案。本文旨在将双调和坐标推广至高阶cage中。

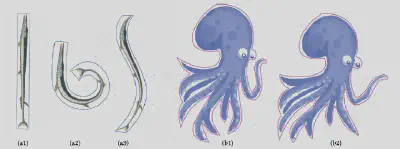
图1. 使用双调和坐标得到的变形结果。支持线性的cage（a1）和高阶cage(b1)，并变形至不同的阶数的高阶cage( a2, a3, b2)。
图1. 使用双调和坐标得到的变形结果。支持线性的cage（a1）和高阶cage(b1)，并变形至不同的阶数的高阶cage( a2, a3, b2)。

解决方案

可以将线性cage内的双调和坐标看作使用边界元法求解区域内的双调和方程的Dirichlet边值问题。

图2. 高阶边界元方法
图2. 高阶边界元方法

基于此，由于cage可以看作是区域边界的一种离散化，本文引入高阶边界元法，实现对区域边界的高阶离散。在高阶边界元法中，区域边界被离散为高阶多项式曲线组成的cage，双调和方程的边界条件被设置为变形后cage的Dirichlet边界条件和Neumann边界条件，并对边界上的未知函数采用高阶基函数来近似，最后联立建立方程组，求解得到双调和坐标。

实验结果

我们对所提出的方法进行了广泛的实验验证。

图3展示了我们方法和线性cage内的双调和坐标的比较，我们的坐标变形结果更光滑，变形方式更直观。

图3. 本文方法与双调和坐标的比较。
图3. 本文方法与双调和坐标的比较。

图4展示了高阶cage相比于线性cage 的优势。高阶cage更贴合形状，变形结果更光滑。

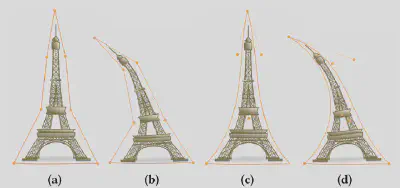
图4. (a)线性cage，(b)使用线性cage的变形结果，（c）高阶cage，（d）使用高阶cage的变形结果。
图4. (a)线性cage，(b)使用线性cage的变形结果，（c）高阶cage，（d）使用高阶cage的变形结果。

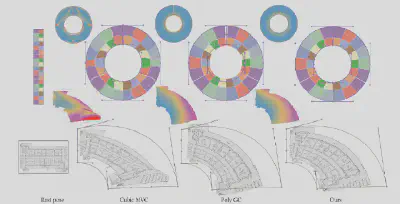
图5展示了和最先进方法的比较，我们的方法在边界对齐和变形扭曲控制之间提供了一个良好的平衡。

图5. 和Cubic MVC和Poly GC的比较结果。
图5. 和Cubic MVC和Poly GC的比较结果。

技术贡献

在这项工作中，我们的贡献主要包括：

1.使用高阶边界元法得到了高阶cage内的双调和坐标。

论文发表

该工作已被计算机图形学顶会SIGGRAPH 2025接收，并将发表于顶级期刊《ACM Transactions on Graphics》。该期刊2024-2025年度影响因子为7.8，是计算机科学与软件工程领域的一区刊物之一。

论文原文

Shibo Liu, Tielin Dai, Ligang Liu, Xiao-Ming Fu. Polynomial 2D Biharmonic Coordinates for High-order Cages. ACM Transactions on Graphics (Proc. SIGGRAPH), 2025.

学术成果