SIGGRAPH 2025-有理参数曲线的广义环绕数的解析表达式

【论文标题】Closed-form Generalized Winding Numbers of Rational Parametric Curves for Robust Containment Queries

【作者】柳士博，刘利刚，傅孝明

【单位】中国科学技术大学

背景与问题

有理参数曲线在计算机图形学，计算机辅助设计与制造领域应用广泛。很多任务，例如动画、模拟和手绘草图，都要求对由一组有理参数曲线包围的区域内部进行显式处理。因此，对这样的区域执行鲁棒且高效的包含查询，即（判断）一个任意空间位置是否包含在该区域内的几何谓词，是至关重要的。同时由于系统误差和手工误差的存在，很多CAD模型和手绘草图不是水密、流形的，针对这类区域进行包含查询，最先进的方法是根据查询点位置对参数曲线进行自适应细分，并通过计算细分后的线段的广义环绕数(GWN)进行鲁棒的包含查询。然而该方法的计算成本取决于曲线的形状和查询点的位置，表现出不稳定的计算速率。

针对这一问题，我们提出了一种新的计算有理参数曲线的GWN的方法，即直接通过解析表达式计算有理参数曲线的GWN。

解决方案

通过推导，计算有理参数曲线和查询点的 GWN 的问题可以轻松地转化为计算多项式曲线的 GWN 的问题。同时，GWN 变成了一个有理多项式的积分。

利用留数定理是获得该积分的解析表达式的核心。我们为该积分设计了特殊的积分函数与积分围道，应用留数定理并进行化简后得到了两个计算该积分的解析表达式。

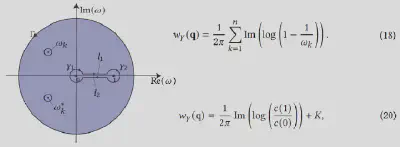
一组有理参数曲线的 GWN 通过将每条曲线的 GWN 相加获得。此外，我们可以轻松地推导出 GWN 的导数，用于其他应用，例如艺术家草图的重新定向。

实验结果

对于我们提出的计算GWN的方法，我们通过对大量的参数曲线与查询点进行实验，比较本文算法与最先进算法的鲁棒性与效率，充分展示了该方法的有效性。 图3展示了本文方法与最先进算法的时间比较结果，本文方法对于2次及3次参数曲线的计算速率是最先进方法的7倍，并且对于不同的查询点的计算时间保持恒定。

图4展示了本文方法在复杂模型上的GWN的计算结果。

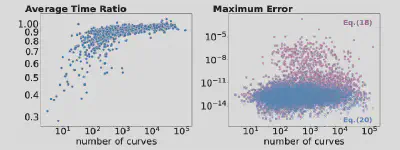
本文也在大规模数据集上验证了方法的有效性。图5展示了在大规模数据集上的加速比率，以及本文提出的两个公式和最先进方法的计算差值。

技术贡献

在这项工作中，我们的贡献主要包括：

1. 将有理参数曲线的GWN的计算与留数定理建立联系，第一次建立了GWN值与多项式的根之间的联系。
2. 得到计算有理参数曲线的GWN的简洁高效的解析表达式，计算速率高效且稳定。

论文发表

该工作已被计算机图形学顶会SIGGRAPH 2025接收，并将发表于顶级期刊《ACM Transactions on Graphics》。该期刊2024-2025年度影响因子为7.8，是计算机科学与软件工程领域的一区刊物之一。

论文原文

Shibo Liu, Ligang Liu, Xiao-Ming Fu. Closed-form Generalized Winding Numbers of Rational Parametric Curves for Robust Containment Queries. ACM Transactions on Graphics (Proc. SIGGRAPH), 2025.