GCL学术成果:SIGGRAPH 2025-TPMS壳晶格超材料优异性能的理论分析与设计
【论文标题】Asymptotic analysis and design of linear elastic shell lattice metamaterials
【作者】张迪,刘利刚
【单位】中国科学技术大学
背景与问题
三周期极小曲面(Triply Periodic Minimal Surfaces, TPMS)作为壳晶格超材料设计中的一类特殊的曲面,具有多方面显著的优点,比如,相互贯通的多孔结构、在较低的材料用量下具有较高的强度和刚度、高比表面积、无应力集中、良好的能量吸收特性等。然而,当前与TPMS物理性质有关的大多数成果仍停留在对少数TPMS结构的数值或实验研究中,尚无法解释其优异性质背后的理论机制,更难以推广到更广泛的曲面种类。TPMS结构在高比强度和高比刚度方面的优异性能的根本原因,依然是一个未解之谜。
本研究以刚度性质作为出发点,引入渐近分析的方法考虑在壳厚趋近于0时等效刚度的渐近行为,来探索中间曲面(中面)几何对壳晶格等效刚度的影响,第一次从理论上证明并解释了TPMS结构为何具有优异的物理性能。
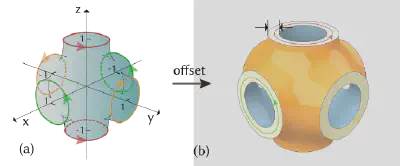
解决方案
我们提出了一种全新的评估指标:渐近方向刚度(Asymptotic Directional Stiffness, ADS)。该指标定义为在壳厚趋于零时,刚度与体积分数之比的极限,它刻画了壳结构的中面几何与其整体刚度之间的本质关系。通过扩展Ciarlet壳理论的部分关键结果,我们推导出了ADS的收敛定理并确定了其计算公式,基于该定理我们建立了ADS的上界及其达到该界的充分必要条件,利用该条件我们首次系统性地解释了TPMS壳晶格在实验中表现出的最优体积模量现象。
论文还引入了一种创新的三角网格离散化方法,克服了使用普通平面单元离散ADS变分方程时出现震荡解的问题(图 2)。

为了将ADS应用在壳晶格设计中,文中提出一种基于能量梯度的几何流算法对曲面的ADS进行优化。由于目标函数的梯度包含高阶导数项,难以在离散网格上计算,文中提出将高阶导数重写为膜应变的形式以利用变分方程消去它们,最终得到了一个适合离散网格计算的梯度形式。在实际优化中,计算得到的能量梯度在线搜索中只允许非常小的时间步长,降低了优化效率。为此,我们利用Laplace算子对该梯度进行预处理。在修正后的梯度下,步长有了大幅提升,优化效率显著提高。
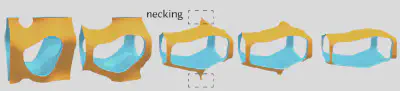
同时,我们发现曲面在演化过程中会出现奇异点(图 3)。为此,我们提出一套策略检测奇异点并通过手术操作去除。
实验结果
我们基于该离散方案测试了对不同的输入曲面和目标函数的优化。图 4展示了对给定的输入曲面优化不同方向杨氏模量的结果,从结果可以看出优化后的杨氏模量在目标方向上有明显提高。
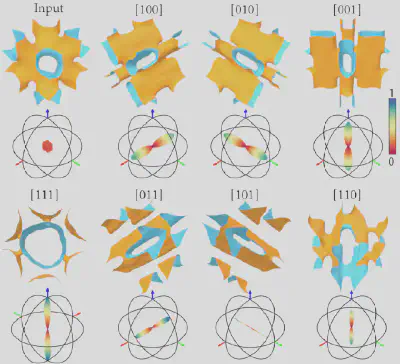
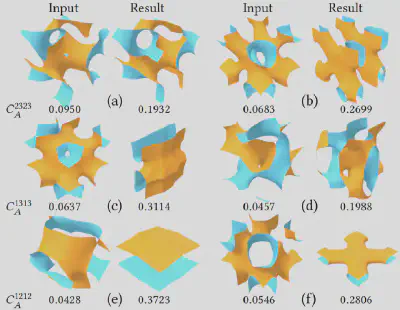
图 5展示了针对不同方向上剪切模量的优化结果,在手术操作下,部分曲面去除了输入曲面拓扑上的障碍演化为了性能更好的形态。
根据达到ADS上限的充要条件,渐进体积模量在曲面为TPMS时达到上限。在数值实验中,不同的输入曲面在优化渐进体积模量后恢复到了TPMS的形状(图 6),相应的目标函数值也逼近了上界(0.3174),符合我们的理论预测。
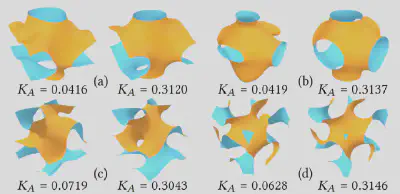
这些数值实验证明,该离散方案能有效提升中面的ADS,在不依赖厚度参数的条件下为工程实践中的壳晶格性能优化提供了新的工具。
技术贡献
在这项工作中,我们的贡献主要包括:
- 提出ADS作为评估壳晶格等效刚度的新理论指标,并严格建立其数学基础;
- 推导出ADS的上限及其实现条件,从理论层面解释了TPMS优异体积模量的来源;
- 针对ADS开发了适用于三角网格曲面的离散化和优化框架,在不需要厚度参数的情况下寻找壳晶格最优的中面。
论文发表
该工作已被计算机图形学顶会SIGGRAPH 2025接收,并将发表于顶级期刊《ACM Transactions on Graphics》。该期刊2024-2025年度影响因子为7.8,是计算机科学与软件工程领域的一区刊物之一。
论文原文
Di Zhang, Ligang Liu. Asymptotic analysis and design of linear elastic shell lattice metamaterials, ACM SIGGRAPH 2025.