GCL学术成果:SIGGRAPH 2025-紧凑三维几何表达
【论文标题】MASH: Masked Anchored SpHerical Distances for 3D Shape Representation and Generation
【作者】李常颢1,辛雨1,周晓巍2,Ariel Shamir 3,张皓4,刘利刚1,胡瑞珍*5
【单位】中国科学技术大学1,浙江大学2,Reichman大学3,SFU 4,深圳大学5
背景与问题
近两年NeRF、3DGS等工作的成功及其在大量领域中的广泛应用充分说明了,更好的3D表示能够极大地推进一个或多个领域的发展,从而反映了“寻找正确的3D表达”的重要性。特别是在三维生成领域中,想要提高生成的几何质量,不仅需要更高精度、更大规模、更多样化的数据支撑,还需要准确、紧凑、结构化、深度学习友好的几何表达。例如,点云无序难以处理,体素内存消耗大,神经隐式表示虽具有连续性和灵活性,SDF、Triplane、Sparse Voxel等表达都在致力于满足三维生成的任务需求,但仍然面临表征能力和紧凑性的取舍问题。
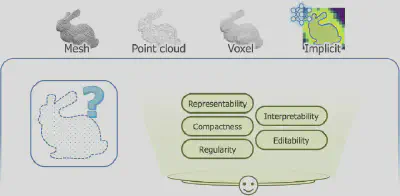
解决方案
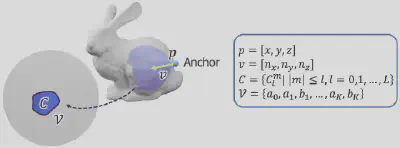
我们提出了一种新颖的基于多视角参数化的三维形状表示:MASH(Masked Anchored SpHerical Distances)。MASH 将 3D 形状表示为一组从固定数量锚点观察到的局部表面补丁集合,每个补丁由球谐距离函数定义,并通过参数化视野锥掩码限制空间范围。如图2所示,对于空间位置p处的锚点,我们定义其朝向为v,然后我们使用三角基函数的系数V来表示该锚点的视野范围,并使用球谐基函数的系数C来表示该锚点到物体表面的距离函数。
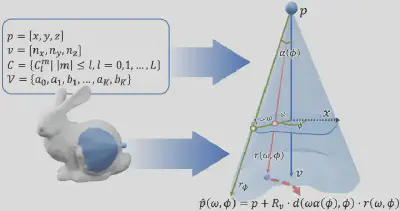
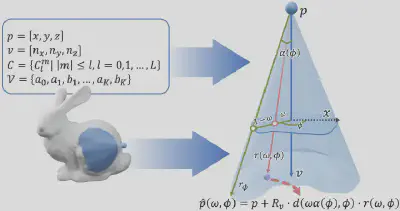
但是,考虑到MASH是对几何分布的高度参数化,因此直接将任意的三维形状转换为MASH表达是具有挑战性的。为此,我们还开发了一种可微优化算法,可以将任意点云转换为精确的 MASH 表示,从而实现高效优化和几何细节适应。具体来说,如图3所示,我们首先在由V定义的自由边界视锥中定义一个参数坐标空间来表示从锚点p出发的任意射线,并将该空间记为(ω,φ)。
以图中红色射线为例,φ表示其与视锥X轴的夹角,ω表示其张角在与X轴具有相同夹角的位于视锥边界上的绿色射线$r_{\theta}$的张角中所占的比例。由于绿色射线可以由V和φ计算得到,而蓝色射线为锚点的朝向v,因此借助该参数坐标空间,我们能够直接从MASH的参数显式地计算得到任意一条图3中所示红色射线所对应的朝向,并通过参数C计算得到的距离值,来得到位于参数化曲面上的点的空间坐标$\hat{p}(\omega,\phi)$。
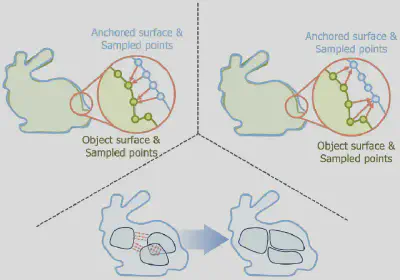
于是,进一步地,我们定义优化目标如图4所示。首先,我们希望MASH上的采样点能够尽可能与给定的三维形状贴合,如左上角所示,我们称其为Fitting Error;同时,我们还希望MASH上的采样点能够将给定的三维形状完全覆盖,如右上角所示,我们称其为Coverage Error;除此之外,由于MASH的目标是使用一组参数化曲面来表示一个物体的完整表面,因此我们希望相邻的参数化曲面的边界尽可能地贴合在一起,如下侧所示,我们称其为Boundary-Continuity Error。
最终,对于任意给定的三维形状,我们能够通过梯度下降来直接优化MASH参数,并使其最终收敛到物体的表面上,如图5所示。
实验结果
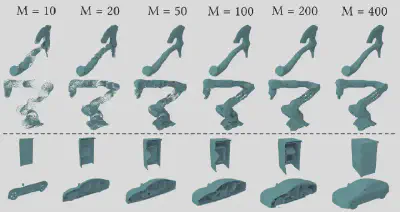
为了验证 MASH 表达的有效性,我们进行了大量的实验。如图6所示,在形状近似实验中,即使只有 10 个锚点,MASH 也能用一组弯曲的参数化曲面忠实地捕捉形状;随着锚点数量的增加,近似误差减小,锐利特征得到更好的保留。除此之外,由于MASH由一组参数化曲面构成,因此可以适应任意的拓扑结构,包括非封闭曲面以及复杂内部结构。
在表面重建任务中,我们将 MASH 转换为网格并与基线方法进行比较,如图7所示,MASH 在光滑性、对输入点云空间分布的贴合度以及恢复复杂几何细节(如薄结构或密集网格)方面优于其他基线方法。

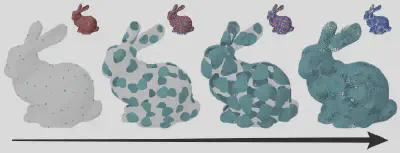
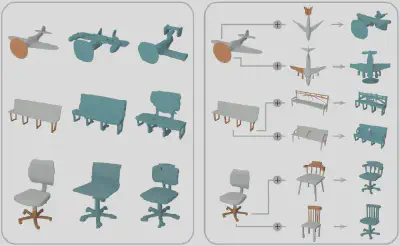
除此之外,由于MASH具有紧凑的几何表示以及规整的数据结构,因此能够很好地被应用于形状生成等任务。这里,我们展示了 MASH 在类别条件生成和图像条件生成两种常见设置下的应用效果。如图8所示,对于类别条件生成,MASH 生成的形状具有更高的多样性和更好的几何细节;如图9所示,对于图像条件生成,MASH 能更好地保持图像中物体的拓扑结构,并更好地恢复完整的几何形状。最后,MASH的局部性还允许我们通过固定一部分参数化曲面,并结合生成模型来实现形状补全或形状混合,如图10所示。


技术贡献
在这项工作中,我们的贡献主要包括:
- 提出了 MASH,一种新颖的基于多视角参数化的三维形状的紧凑表示,能够准确捕捉任意几何和拓扑的物体表面。
- 提出了一种可微的 MASH 优化算法,能够将任意输入点云转换为精确的 MASH 表示。
- MASH 支持多种应用,包括形状生成、补全、混合和重建。在重建方面,MASH 的局部性和每个参数化曲面的高表达能力以及光滑性使其能更好地捕捉局部细节。
论文发表
该工作已被计算机图形学顶会SIGGRAPH 2025 Conference Track接收。
论文原文
Changhao Li, Yu Xin, Xiaowei Zhou, Ariel Shamir, Hao Zhang, Ligang Liu, Ruizhen Hu. MASH: Masked Anchored SpHerical Distances for 3D Shape Representation and Generation. ACM SIGGRAPH 2025 Conference Proceedings.