GCL学术成果：SIGGRAPH 2025-分治嵌入

【论文标题】Divide-and-Conquer Embedding

【作者】程元元，方清*，刘利刚，傅孝明

【单位】中国科学技术大学

背景与问题

三角网格的平面参数化是计算机图形学的基本任务，在保持全局或局部单射性的同时确保低扭曲，对许多应用至关重要。现有方法通常从一个满足双射的初始化出发，通过优化扭曲能量并始终满足双射条件来实现此目标。生成此类初始化最著名的方法是 Tutte嵌入，理论保证其在无限精度计算时双射严格成立。然而这类方法的数值实现通常依赖于浮点精度求解线性方程组，这在处理复杂网格时由于数值误差可能会产生违反全局单射的结果；如果提升数值计算精度，则计算时间与运行内存均会显著增加，在精确数算法下求解线性方程组在个人计算机上目前还难以实现。为避免理论保证失效，近期研究聚焦于设计与精确算术兼容的构造性算法。虽然这些方法能够在线性时间复杂度内生成单射映射，但其适用范围受限：Finnendahl等提出的E3A算法仅支持三边形区域映射；Livesu针对凸多边形域提出了以条带构建嵌入方法，但该方法无法处理含不可收缩边的网格，且预处理阶段需对所有不可收缩边进行切割操作。因此设计一种理论上将拓扑同胚于圆盘的三角网格双射参数化到任意凸多边形域的构造方法是一个尚未解决的问题。

解决方案

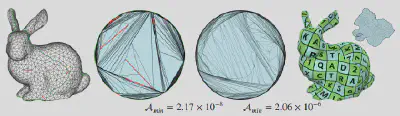
我们提出一种基于分治思想的构造方法。该方法将三角网格和具有固定边界的凸多边形域的映射问题递归分解为子三角网格和子凸多边形域的映射问题，并逐对进行处理，对该过程持续迭代直到每个子网格仅包含单个不可再分的三角面片。

每次分解包含凸域分解、寻找可行路径与建立新边界映射三步。具体地，对每个凸多边形域进行凸域分解，通过在凸多边形边界上寻找成对边界点并利用连接成对边界点的线段对凸域划分得到；接下来，利用算法在三角网格上寻找对应该连接成对边界点的线段的可行路径，最后将此可行路径上的顶点双射到凸域分割线段上。

我们证明从初始建立三角网格边界与凸多边形域边界的双射之后，每次分解依次按某些分类标准进行判断并进行相应处理，一定可以分解到不可再分的三角面片情形，进而完成双射嵌入。以上构造步骤从理论上能够保证双射，同时在构造过程中只涉及网格顶点在凸域分割线段上的插值，所以该方法能够兼容各种数值精度与精确算术。

实验结果

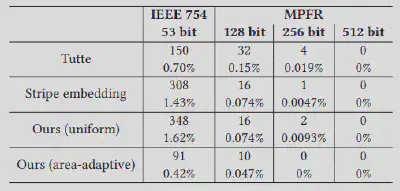
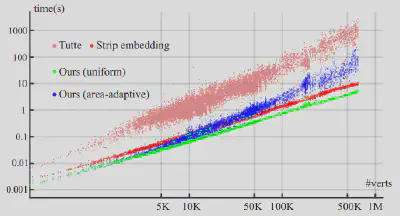
我们在包含21.4K个三角网格的数据集上进行了测试，精确算术上我们的方法均实现了双射嵌入，这验证了我们方法的鲁棒性和有效性。如表1所示，我们与其他方法进行了结果有无翻转的比较。可以看出，在相同精度下，面积自适应权重插值的无翻转个数较其他方法更少，均匀权重与目前最新基于构造的条带嵌入方法效果相当。图2展现对应MPFR 512精度下与其他方法的时间比较，均匀权重分治嵌入方法较其他方法更快。

表1. 在 21.4K 个网格上，使用固定精度时Tutte嵌入方法、条带嵌入方法、我们均匀权重分治嵌入方法（Ours (uniform)）和我们面积自适应权重分治嵌入方法（Ours (area-adaptive)）的有翻转个数统计。

技术贡献

在这项工作中，我们的贡献主要包括：

1.  基于分治思想构造了一种理论上保证双射的平面参数化方法。
2.  兼容各种数值精度和精确算术，且不会因数值精度的提高显著增加时间。

论文发表

该工作已被计算机图形学顶会SIGGRAPH 2025接收（conference track）。

论文原文

Yuan-Yuan Cheng, Qing Fang, Ligang Liu, Xiao-Ming Fu. Divide-and-ConquerEmbedding. In ACM SIGGRAPH 2025 Conference Proceedings, 2025.