GCL学术成果:SIGGRAPH 2025-基于高阶控制结构的三维网格变形格林坐标
【论文标题】Flexible 3D Cage-based Deformation via Green Coordinates on Bézier Patches
【作者】肖冬,陈仁杰*
【单位】中国科学技术大学
背景与问题
三维网格变形是计算机图形学中的基本问题,其中一大类方法是基于笼(cage)的变形,即在网格周围建立包围网格曲面的笼子结构,并将笼子结构包围的空间中任意一点的坐标表达为笼顶点坐标的加权组合。随着源笼变形为目标笼,嵌入三维空间的网格也会随之发生变形。在空间三维变形中,前人方法通常使用三角形或四边形网格作为笼结构,而它们要么具有线性结构,要么具有线性的等参曲线,对于复杂,弯曲,高曲率的变形控制能力有限。
解决方案
本文观察到Bézier曲面(包括张量积Bézier曲面,Bézier三角形等)具有高阶结构,且具有非线性的等参曲线,因而提出利用Bézier曲面作为控制笼,并在Bézier笼上建立格林坐标,实现具有一定保形性的三维网格变形。本文进行了连续情况下的坐标推导,将坐标建立在Bézier曲面控制网格的顶点和法向上,并求得Bézier笼上格林坐标的积分表达式。由于该积分不具有显式的原函数,本文将参数区域细分,并进行数值近似计算,同时,由于数值积分会产生一定的误差,本文提出全局解空间投影法,使得坐标精确满足线性重构性质(linear reproduction),且Dirichlet项精确满足单位分解性质(partition of unity)。
实验结果
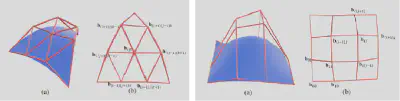
下图的左,右例子分别展示了使用张量积Bézier曲面以及Bézier三角形作为笼结构的变形结果。

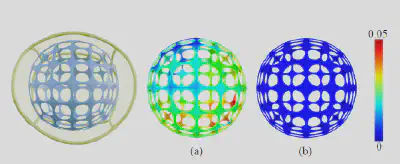
下图展示了全局解空间投影的效果。(a)图表明数值积分产生了一定的误差,(b)图表明解空间投影后的坐标精确满足线性重构性质。
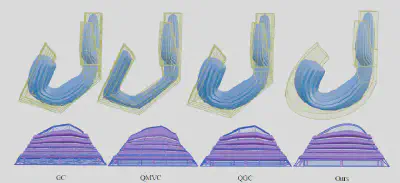
下图展示了更多的实验结果。
技术贡献
在这项工作中,我们的贡献主要包括:
- 首次在具有曲边边界的三维高阶Bézier笼上建立格林坐标,实现灵活,弯曲,高曲率的变形。
- 提出全局解空间投影法,使得经数值积分近似计算的坐标,在投影后能精确满足线性重构性质,且Dirichlet项精确满足单位分解性质。
论文发表
该工作已被计算机图形学顶会SIGGRAPH 2025 conference track接收。
论文原文
Dong Xiao, Renjie Chen. Flexible 3D Cage-based Deformation via Green Coordinates on Bézier Patches. In ACM SIGGRAPH 2025 Conference Proceedings, 2025.