【论文标题】Constructing boundary-identical microstructures via guided diffusion for fast multiscale topology optimization

【作者】冯靖轩1，王莉莉1，翟晓雅1，陈凯2，吴文明3，刘利刚1，傅孝明1

【单位】中国科学技术大学1，中关村人工智能研究院2，合肥工业大学3

背景与问题

力学微结构因其独特的力学特性而备受关注，这些特性源自其特有的拓扑设计。基于这些微结构构建的多尺度系统能够实现一些复杂的功能，如隐形斗篷、软体机器人及高热导率的设计等。尽管现代制造技术的发展已使宏观和微观尺度上创建这些复杂系统成为可能，但设计这样的多尺度系统依旧充满挑战，尤其是在逆向设计微观结构以及执行昂贵的多层次优化过程方面。

随着计算能力的增强和机器学习方法的进步，数据驱动的多尺度优化逐渐成为重要的设计手段。当前的数据驱动多尺度设计框架主要分为两大类：自顶向下和自底向上方法。自顶向下方法首先通过拓扑优化确定宏观属性分布，然后使用预先生成的微观结构数据库来填充设计方案。相反，自底向上方法则以体积分数等参数作为设计变量，并利用机器学习模型预测有效属性以加快优化流程。不过，自底向上方法中使用的参数化表示可能会限制微观结构属性的空间范围，因此在多尺度设计时，我们倾向于采用自顶向下方法。但在设计过程中，我们需要满足两个关键要求：边界连通性好和弹性模量范围大，这意味着需要构建具有相同边界且覆盖广泛弹性张量范围的微结构数据集。

然而，生成这样的微结构数据集面临两大挑战：一方面，传统拓扑优化算法产生的结构多样性不足，加上对边界连通性的严格约束，这进一步缩小了微结构弹性模量的范围；另一方面，选择一个合适的边界类型以确保生成的微结构拥有广泛的弹性模量范围是相当困难的。

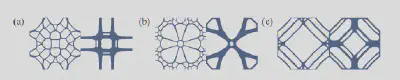
解决方案

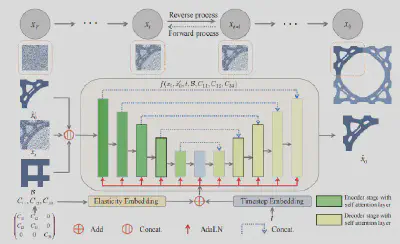
为了构建具有一致边界且覆盖广泛属性范围的微结构数据集，我们采用条件扩散模型来生成特定边界和弹性张量的微结构，并通过以下主动学习策略迭代地扩充该数据集：

1. 利用生成的边界一致的数据集对条件扩散模型进行训练；
2. 借助训练好的模型进行采样，并将采样得到的结果整合到现有数据集中。

通过上述步骤的多次循环迭代，我们能够逐步扩展微结构属性的覆盖范围，从而获得一个更加丰富多样的微结构数据集。这种方法不仅确保了新生成的微结构在边界上的一致性，同时也有效地探索了更广泛的弹性模量范围，增强了数据集的多样性和实用性。

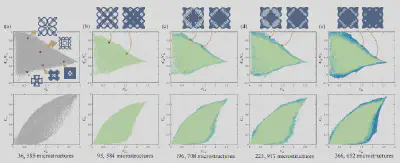
实验结果

基于以上方法，我们构造了边界一致的大范围微结构数据集。

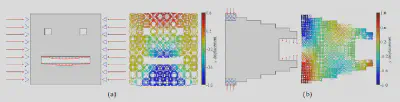
我们利用生成的数据集实现了机械斗篷和指定变形结构的高效设计。在多尺度设计的过程中，相较于以往的方法，我们避免了对微结构间边界兼容性进行极为耗时的优化步骤，从而将多尺度设计所需的时间减少了99%以上。实验结果充分展示了我们所构建的微结构在多尺度设计中的有效性和高效性。这一进展不仅大幅提升了设计效率，同时也保证了最终设计结果的性能和可靠性。

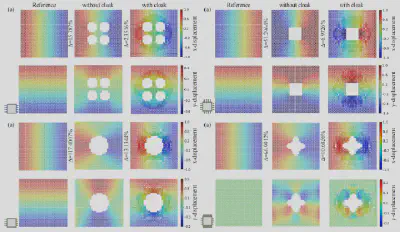
研究贡献

在这项工作中，我们的主要贡献包括：

1. 成功构建了一个边界一致且覆盖广泛属性范围的微结构数据集，首次验证了此类数据集的构造可行性。
2. 基于所构建的边界一致大范围微结构数据集，我们提出了一种多尺度优化策略，显著提升了多尺度设计的效率。

论文发表

该工作将发表于计算力学领域的顶级期刊《Computer Methods in Applied Mechanics and Engineering》。该期刊2023-2024年度影响因子为6.9，是工程技术领域的一区刊物之一。

论文原文

Jingxuan Feng+, Lili Wang+, Xiaoya Zhai*, Kai Chen, Wenming Wu, Ligang Liu, Xiao-Ming Fu*. Constructing boundary-identical microstructures via guided diffusion for fast multiscale topology optimization. Computer Methods in Applied Mechanics and Engineering, 2025.