GCL学术成果:SIGGRAPH Asia 2024 — 曲线区域上的多项式柯西坐标
【论文标题】Polynomial Cauchy Coordinates for Curved Cages
【作者】林哲晖,陈仁杰
【单位】中国科学技术大学
【背景与问题】
在计算机图形学领域,重心坐标广泛应用于形状变形等问题。传统的重心坐标主要定义在多边形域上,边界由直线段表示。然而,使用曲线表示域边界可以提供更高的灵活性和保真度,这在众多应用场景中具有关键意义。
近年来,研究者们提出了多种方法来推广重心坐标到曲线边界。其中,二维多项式格林坐标(PGC)实现了目标cage采用多项式曲线的突破,但源cage仍局限于多边形形式。另一项较早研究《Cubic Mean Value Coordinates》则通过引入中间步骤,成功实现了曲线区域之间的变形,但该方法仅支持最高三阶的曲线。
【解决方案】
本文提出了一种新的多项式柯西坐标,旨在实现曲线区域上的形状变形。我们使用分段Bézier曲线表示域的边界,成功将柯西复重心坐标推广到曲线边界的情况,与现有二维多项式格林坐标相比,我们的方法能得到等效的结果。同时,通过推导坐标的任意阶导数表达式,以及基于柯西积分公式推导出的逆映射的数值积分公式,我们可以通过中间步骤实现曲线包围区域之间的变形。这使得我们拥有更灵活的输入选择,可以直接使用曲线cage作为输入。

本文方法不仅解决了传统重心坐标在处理多边形边界时的局限性,还提供了一个既灵活又高效的形状变形工具。
【实验结果】
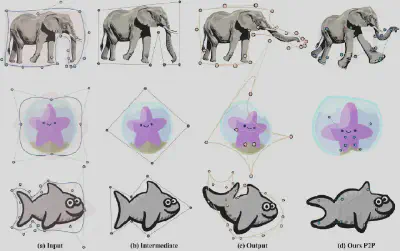
我们对所提出的方法进行了广泛的实验验证。在输入是直边的情况下,我们的结果与二维多项式格林坐标(PGC)的差异仅在数值精度范围内,实验上证实了两种方法的等价性。而在输入是曲边的情况下,本文方法同样能够产生保形的变形结果。我们通过大量实验展示了该坐标在交互式变形中的有效性和灵活性。
【技术贡献】
在该项工作中,主要贡献包括:
1、将现有的柯西复重心坐标推广到多项式情况,并提供了解析表达式
2、基于Bézier形式构建坐标表达式,使用户能够通过操纵控制多边形顶点,实现对目标曲线的交互式编辑
3、推导给出了坐标的任意阶导数表达式,这可以用于P2P约束变形和平滑能量驱动的变形等应用4、推导给出了逆映射的表达式,通过中间步骤实现了曲线包围区域之间的变形
【论文发表】
该工作已作为会议论文被计算机图形学顶会SIGGRAPH Asia 2024接收。
【论文原文】
Zhehui Lin, Renjie Chen. Polynomial Cauchy Coordinates for Curved Cages. ACM SIGGRAPH Asia 2024 Conference Proceedings.