GCL学术成果:SIGGRAPH Asia 2024-多点共轭机构
【论文标题】mpcMech: Multi-Point Conjugation Mechanisms
【作者】陈柯1,李斯祺2,宋鹏2,郑建民3,刘利刚1
【单位】中国科学技术大学1,新加坡科技设计大学2,南洋理工大学3
【背景与问题】
机械结构(Mechanism,简称机构)是由通过关节连接的运动部件组成的,用于将输入运动(通常是单自由度的旋转运动)转换为所需的输出运动。基础机构只能产生比较简单的运动,例如凸轮机构可以生成线性运动。为了生成更为复杂的运动,传统的方法是通过组合多个基础机构(包括连杆机构、凸轮机构和齿轮副)来建模一个复合机构。这些复合机构通常具有较为复杂的拓扑结构,这将增加其装配和维护的复杂性。此外,我们也有理由假设,由于各部件制造误差的累积,复杂的拓扑结构也会降低这些复合机构所生成运动的功能性。
为了克服传统机构的这种局限性,一种新兴的方法是建模具有简单拓扑结构的机构,但其仍能够传递复杂的运动;其核心思想是将复杂的运动信息“编码”进机构的几何之中。随着增材制造技术的发展,具有自由几何(freeform geometry)的机构可以用3D打印技术方便且廉价地制造。然而,建模自由几何的机构用以生成用户指定的运动仍然是一项具有挑战性的任务。最近,一些学者试图通过推广三维凸轮机构和齿轮副的几何来解决这一挑战。然而,这些机构只能产生具有有限复杂性的运动,例如在2-自由度的运动空间中实现球面上的路径。
针对这一问题,我们的目标是从共轭曲面(conjugate surface)的角度设计自由几何机构,从而生成更复杂的运动。

【解决方案】
为了避免复杂的拓扑结构,本文研究了仅由一对运动部件构成的机械结构,将其用于生成复杂的运动。本文将该对运动部件建模为一对具有多个共轭点的共轭曲面,从而形成多点共轭机构(mpcMech)。为了研究这种新型机构,我们将共轭曲面理论与形封闭抓取理论建立联系,提出了动态形封闭条件(dynamic form closure condition)。在此条件下,一个共轭曲面通过多个共轭点能够连续不断地将运动传递给另一个共轭曲面。基于此条件,我们提出了一种基于优化的方法来建模多点共轭机构的几何,用以精确生成用户指定的运动;该方法适用于一维、二维或三维的运动空间。该方法的核心在于对满足多点共轭、动态形封闭和可制造性等各种要求的多对共轭曲线进行建模。更多细节与说明详见我们的论文。
【实验结果】
对于我们提出的建模多点共轭机构的方法,我们通过对不同类型的多点共轭机构建模并生成各种运动、使用3D打印原型评估机构的运动学性能、展示了这种机构的三个应用实例,充分展示了该方法的有效性。

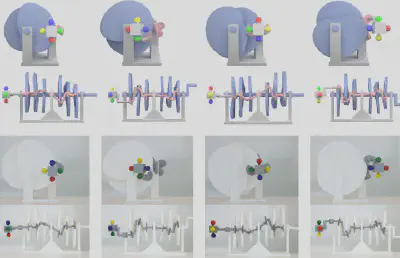
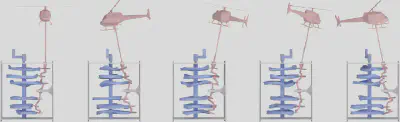
【技术贡献】
在这项工作中,我们的贡献主要包括:
- 将共轭曲面理论与形封闭抓取理论建立联系,提出了机械结构的动态形封闭条件。
- 基于上述的条件,提出了一种基于优化的方法来建模多点共轭机构的几何,以精确生成用户指定的运动,所生成的运动可达3-自由度。
【论文发表】
该工作已被计算机图形学顶会SIGGRAPH Asia 2024接收,并将发表于顶级期刊《ACM Transactions on Graphics》。该期刊2023-2024年度影响因子为7.8,是计算机科学与软件工程领域的一区刊物之一。
【论文原文】
Ke Chen, Siqi Li, Peng Song, Jianmin Zheng, and Ligang Liu. mpcMech: Multi-Point Conjugation Mechanisms. ACM Transactions on Graphics (Proc. SIGGRAPH Asia), 43(6),2024.
【论文主页】
https://sutd-cgl.github.io/supp/Publication/projects/2024-SIGAsia-mpcMech/index.html