GCL学术成果：IEEE TPAMI 2025-高效高精度非刚性配准

8月 27, 2025 1 分钟阅读时长

【论文标题】SPARE: Symmetrized Point-to-Plane Distance for Robust Non-Rigid 3D Registration

【作者】要宇馨1,3，邓柏林2，侯军辉3，张举勇1

【单位】中国科学技术大学1，卡迪夫大学2，香港城市大学3

背景与问题

精准感知与高效处理空间信息，是实现空间智能应用自动化和智能化的核心能力。无论是在卫星遥感、无人机测绘、机器人导航还是增强现实（图1）等场景中，都离不开对三维空间的高精度建模与分析。作为空间智能的关键基石，三维配准技术将不同时间、不同视角或不同传感器获取的点云、图像及模型数据，精准对齐至统一坐标系，从而实现多源数据的无缝融合与一致性表达。当前，随着传感技术的飞速发展、计算硬件性能的大幅提升以及算法的持续优化，三维配准技术正不断突破精度与适用场景的边界，成为推动空间智能应用向更广领域、更高精度迈进的核心驱动力。

图1. 三维配准在空间智能中的应用，图片为AI生成。
图1. 三维配准在空间智能中的应用，图片为AI生成。

三维配准技术的核心挑战在于如何在未知点对应关系的条件下，精准求解相对变换。根据物体形变特性，配准任务可分为两类：

● 刚性配准：处理平移旋转不变的物体（如场景中的家具、建筑等）

● 非刚性配准：处理动态形变物体的空间对齐（如运动生物、铰链式的机械结构、软体物质等）

由于需对复杂形变进行建模，非刚性配准面临更为严峻的技术挑战（图2）。其核心难点在于如何构建能够适应多样化变形的变形场，以及在形变条件下仍能建立稳定、准确的对应关系。突破非刚性配准的关键瓶颈，将为下一代空间智能应用提供更精准、更实时的感知能力，推动技术在复杂动态场景——如自动驾驶、柔性机器人、活体医疗检测等领域的广泛应用与落地。

图 2. 非刚性配准示例，其中源表面以非刚性方式变形以与目标匹配及对齐。
图 2. 非刚性配准示例，其中源表面以非刚性方式变形以与目标匹配及对齐。

传统非刚性配准方法长期面临三重挑战：

● 数据质量缺陷：扫描中的噪声与缺失易导致配准偏差；

● 复杂异构形变：曲面结构扭曲削弱特征对应可靠性，而形变多样性（如近刚性变化、布料褶皱、肌肉运动等）也加大基于先验的对应点学习难度；

● 效率与精度难以兼顾：不准确的曲面距离近似与冗余形变自由度，使高精度与高效率无法同时实现。

解决方案

针对全局对应不可靠的问题，我们转向局部配准范式，以降低初始化依赖、聚焦精细对齐。配准效果高度依赖于误差度量方式，因此引入对称点对面距离，借助其近似二阶收敛特性提升效率。但该方法仍面临三大挑战：

● 复杂形变下法向估计困难；

● 高自由度变形易产生“伪对齐解”；

● 噪声、离群点和局部缺失降低度量有效性。

为此，本文提出SPARE方法，通过三项创新系统性应对上述问题：

√ 法向估计优化：结合尽可能刚体正则化假设，联合优化局部形变约束与对称距离，提升法向准确性；

√ 消除冗余自由度：采用基于变形图的层级粗对齐策略，保留源曲面特征的同时降低优化自由度，杜绝伪对齐；

√ 噪声自适应抑制：设计基于几何一致性的自适应权重机制，动态抑制不可靠对应点，增强鲁棒性。

此外，为有效求解高度非线性优化问题，我们设计了一种适配的求解算法，将复杂优化分解为多个可闭式求解的子问题，确保高效收敛，并有效规避局部最优解的困扰。通过上述改进，SPARE方法为非刚性配准中的法向估计、自由度优化及噪声干扰等问题提供了系统化解决方案。更多技术细节详见论文：https://arxiv.org/abs/2405.20188。

实验结果

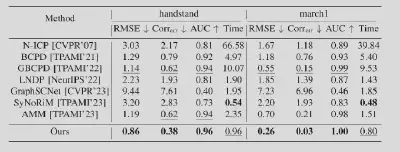
提出的方法在合成与真实数据集上均实现了高的配准精度，如图3，图4与表1，展现了所提出方法在配准精度与速度方面的优越性。

图3. 我们方法在非刚性跟踪上的结果展示。
图3. 我们方法在非刚性跟踪上的结果展示。

图4. 我们方法与现有方法在匹配准确性上的比较，纵坐标数值越大越好。
图4. 我们方法与现有方法在匹配准确性上的比较，纵坐标数值越大越好。

表1. 我们方法与现有方法的数值结果比较。
表1. 我们方法与现有方法的数值结果比较。

技术贡献

  1. 提出基于鲁棒点到平面距离和局部刚性正则化的精配准算法，大幅提升精度并降低初值依赖；

  2. 设计由粗到细的层级化变形建模，实现高效求解，避免局部最优，同时精确对齐局部曲面；

  3. 通过交替优化和设计代理函数，简化复杂问题求解，显著提升效率；

  4. 提出的方法在所有数据集上均实现了显著领先的配准精度（例如表1中，match1序列的RMSE误差仅为SOTA方法的一半），同时运行速度全面优于所有基于优化的对比方法。

论文发表

该工作已被IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI) 接收。

论文原文

Yuxin Yao, Bailin Deng, Junhui Hou, Juyong Zhang. SPARE: Symmetrized Point-to-Plane Distance for Robust Non-Rigid 3D Registration. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2025.

论文主页

https://github.com/yaoyx689/spare

系列工作

近年来，张举勇教授课题组在三维配准方向展开了系列研究工作，包括：

  1. 高效高精度刚性配准算法，提出了新的优化配准度量函数与优化方案，显著提升了刚性配准精度与速度。
  • Zhang et al. Fast and Robust Iterative Closest Point. TPAMI, 2022.

Code: https://github.com/yaoyx689/Fast-Robust-ICP

  1. 用于鲁棒局部配准的非刚性配准算法，设计了对曲面网格质量极小依赖的变形图建图策略，及针对问题特性的建模与高效求解。
  • Yao et al. Quasi-Newton Solver for Robust Non-Rigid Registration. CVPR 2020. Oral presentation.

Code: https://github.com/Juyong/Fast_RNRR

  • Yao et al. Fast and Robust Non-Rigid Registration Using Accelerated Majorization-Minimization. TPAMI 2023.

Code: https://github.com/yaoyx689/AMM_NRR

  1. 最近，针对全局刚性配准问题，我们提出了在特征空间/局部几何双空间的优化框架DualReg[1]，在配准精度与计算效率方面取得了显著提升。在不损失配准精度情况下，我们方法的计算速度为MAC[2]方法的32倍。

[1] Li et al. DualReg: Dual-Space Filtering and Reinforcement for Rigid Registration. https://arxiv.org/abs/2508.17034

[2] Zhang et al. 3D Registration with Maximal Cliques. CVPR 2023, best student paper award.